各放射線の特徴について：α線、β線の飛程の求め方

α線とβ線の飛程の求め方についてまとめますが、通常使用される細かい式と粗い式との差についても検討してみます。

令和元年、2年8月問5（同じ問題）

選択肢1

「⁹⁰Srの壊変核種である⁹⁰Yからのβ線の空気中における最大飛程は, 5mを超える.」

選択肢4

「α粒子は人体組織中で数十μm程度の飛程を持つが, この距離で全エネルギーを失うことから比電離は大きい.」

これらについて両方とも正しい。

ここではまず、α線とβ線の飛程を求めます。

α線は以下の式で求めます。

エネルギーの範囲は4 ~ 7 MeV において用いられます。

（アイソトープ手帳第12版 p5参照）

荷電粒子の飛程まとめ – 放射線取扱主任者試験対策(物理化学生物)ブログ (hatenablog.com)より引用

これを試験では関数電卓を使わずに一般の電卓で求めることは難しいので、この問題ではおそらく感覚としてα粒子の飛程を覚えていることが要求されていると思われます。

（問題が変わっていないことから過去問を解いているうちに自然に覚えてしまうということもありそうです。）

ここでは概算であればR=0.5E(β線の遮蔽のための粗い飛程を見積もる式と同様の考え方(荷電粒子と物質の相互作用 – 放射線取扱主任者試験に合格しよう！ (hatenablog.com))でも良いのではないかと考え、教科書通りの式と比較します。

まず、普通の式から算出します。

α線のエネルギーは例えば単位としてはMeVなので、ここでは

E = 5MeVとして計算します（しきい値の関係からか理由は分かりませんがα線のエネルギーは3~7MeVが多いようです）。

①式から空気中での飛程は、

R = 0.338 × 5^3/2 = 3.779 cm

これを②式においてR₀として

人体の密度は水とあまり変わらないですが、ここではwikipediaから参考にして、ρ = 0.985 g / cm³として計算します。

また、同様に空気の密度を ρ₀ = 1.293 × 10^-3 g cm^-3 とします。

さらに空気と水の質量数について、

空気は 窒素N : 酸素O = 4 : 1 として平均を求めるとその質量数は

A₀ = 14 × 4/5 + 16 × 1/5 = 14.4

水H₂0は 水素H : 酸素O = 2 : 1 となるので

A = 1 × 2/3 + 16 × 1/3 = 6

参考：密度の比較 – Wikipedia

以上の数値を代入して

R=ρ₀ / ρ × √ (A / A₀ ) × R₀

= 1.293 × 10^-3 g cm^-3 / 0.985 g / cm³ × √ (6 / 14.4)

× 3.779 cm

= 3.20 × 10^-3 cm = 3.20 × 10^-5 m = 32.0 μm

このように、選択肢4の数十μmと合っていることが分かります。

試験や実務、暗算でだいたいの間隔を掴むための概算であれば計算を簡単にすることができます。

先述の通りα線のエネルギーは3 ~ 7 MeV 程度ですがもしこの値を忘れていたとしてもMeVオーダーだと覚えていれば1MeVとして、先述のR=0.5Eを用いて、

R = 0.5 × 1 = 0.5 cm

これを②式においてR₀として,　水の密度はρ = 1、空気の密度は水のだいたい1/1000としてρ₀ = 1× 10^-3 g cm^-3、さらに質量数は空気は窒素のみと考えてA₀ =14, 水はA=10とした場合に√ (A / A₀ )=1という粗い近似で計算すると

R=ρ₀ / ρ × √ (A / A₀ ) × R₀

= 1 × 10^-3 g cm^-3 / 1 g / cm³ × 1 × 0.5 cm

= 0.5 × 10^-3 cm = 5 × 10^-6 m = 5 μm

よって、オーダーで見積りたいときにはかなりざっくりした乱暴な近似をして計算を簡単にするのが時間短縮になって良いのではと思います。

次に、β線の飛程について以下の式の通りとなります。

計算すると、

R = 0.542 × E₂ – 0.133

= 0.542 × 2.28 – 0.133

= 1.10 (g cm^-2 )

空気の密度で除すると、

R = 1.10 g cm^-2 / 1.293 × 10^-3 g cm^-3

= 853 cm = 8.53 m

よって選択肢1の5mを超えるが確認できました。

先述の通り、遮蔽計算等に粗く見積もる場合はR=0.5Eも用いられていることからで計算してみます。

R = 0.5 × E

= 0.5 × 2.28

= 1.14 (g cm^-2 )

空気の密度で除すると、

R = 1.14 g cm^-2 / 1 × 10^-3 g cm^-3

= 1140 cm = 11.4 m

オーダーでの確認はこちらでも問題なさそうです。

ところで、先ほどから用いているR=0.5Eと厳密な式はどのくらい離れているのかについて確認してみます。

α線は4~7 MeV、β線は0.05 ~ 10 MeVのエネルギー範囲で0.05 MeVごとにプロットし折れ線グラフとしました。

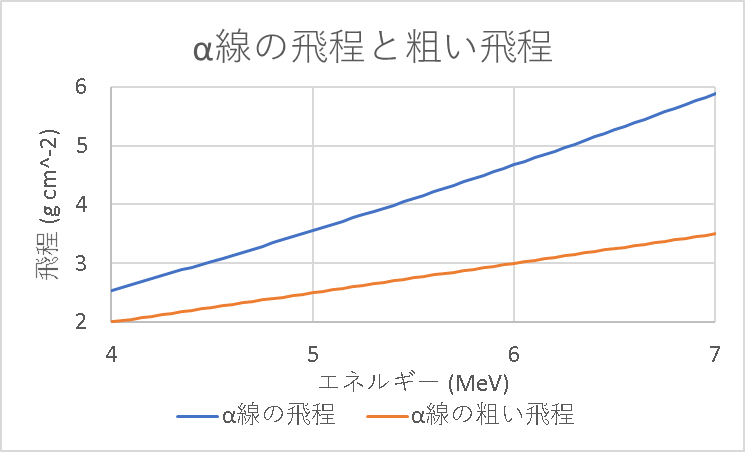
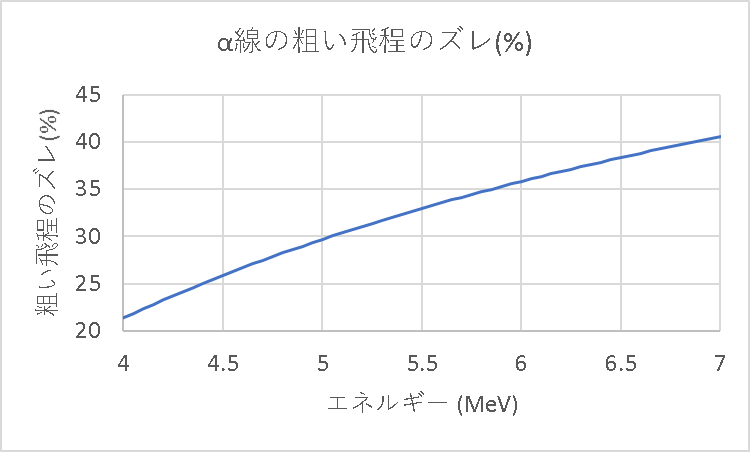
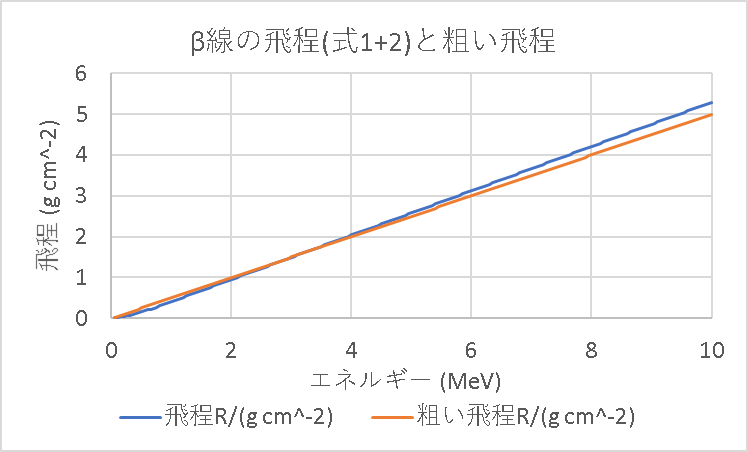
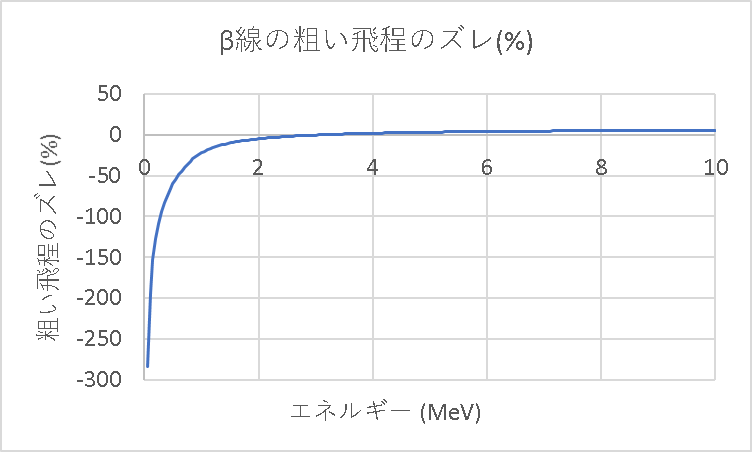
以上のようになりましたが試験や遮蔽計算等でどれだけの精度を求めるかによって式を使い分けると良さそうです。

興味があれば自分でグラフを作っても面白いかと思います。

以上、参考になれば幸いです。