月: 2022年3月

全体を理解して解くのは難しいので解き方、考え方を列挙していきます。学術的には正しくないこともあるかと思いますが試験攻略が目的ということでご容赦願います。

また、ガスクロマトグラフの概要、原理や装置の構成等はまとめた他のサイトがいくつもあると思いますのでそちらを参考にしてください。本ブログでは他のサイトでざっくり原理や構成について知った上で試験問題にどう適用するかの橋渡しとなればと思います。

まず、キャピラリーカラムの理論段数について(令和2年8月問12, 平成31年2月問18)

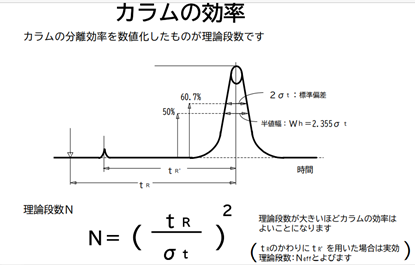
→ここで理論段数(n)とは固定相と移動相との間で分離を行う装置の性能を表していて、簡単に言うと分液漏斗による分離を何回やるかに対応するというイメージです。

この①分液漏斗のイメージと②管のイメージの両方を使い分ければ簡単に考えられます。

（理科等で分液漏斗を使ってない人にはわかりずらいかもしれませんが長いキャピラリーの中で連続的に何回も分離操作が行われているのがクロマトグラフだと考えてもらえればと思います。）

①分液漏斗のイメージで考える選択肢↓

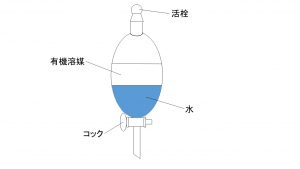
・測定対象物質ごとに異なる

分液漏斗でどの物質を分離するかで分配比は変わることをイメージします。

・キャリアーガス流量により異なる

→分液漏斗に使用する溶媒（ガス流量）が多いほど分離が良くなる=理論段数が大きくなるということです。

・固定相の種類により異なる

→分液漏斗で使用する有機溶媒（固定相）を変えると分配比は変わります。

・カラム温度により異なる

→分液漏斗のイメージで、分離の際に温度が変化すると有機相と水相（移動相と固定相）の溶解度がそれぞれ変化する→分配比が変わるイメージです。

・カラム長が長いほど大きくなる

長い分だけ分液漏斗の分離操作の回数が増えるイメージです。

②管のイメージで考える選択肢↓

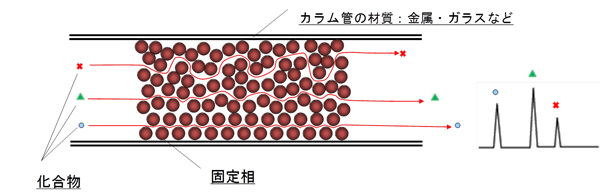
・カラムの膜厚が大きいほど小さくなる

膜厚が大きいと脱着に時間を要するので

・カラム内径が小さいほど大きくなる

→内径が小さい方が内壁に吸着されやすくなるので

・移動相の流速に依存する

→速すぎると内壁に吸着する間もなく流れてしまうイメージです。

続いて、カラムの長さを2倍にしたとき、ピークの形状やカラム性能（カラム特性）はどうなるか？(令和3年2月問18、令和2年2月問18)

・ピーク面積は変化しない

→物質量に関係するものなので変化しない

・理論段数は2倍になる

・理論段相当高さは変化しない

→ 理論段相当高さH = カラムの長さL / 理論段数n であり、

Lを2倍にするとnも2倍になる

よってH(理論段相当高さ)は変化しない

・保持時間は2倍になる

→保持時間t_Rは試料をカラムに注入してピークが現れるまでの時間

・ピーク幅は√2倍になる

→ ピーク幅Wとして、n = (4 t_R / W )² の関係があるのでnもt_Rも2倍にした時、上記の変形した式

W = 4 t_R / √n に代入して　W’ = 4 × 2 t_R / √(2n)

= 4√2 t_R / √n = √2 W

上記のように導出するのは難しいと思いますので

試験では2倍か、変化しないのどちらか直感で分かるものでないなら√2倍になりそうと考えれば良いかも

・分離度は√2倍になる

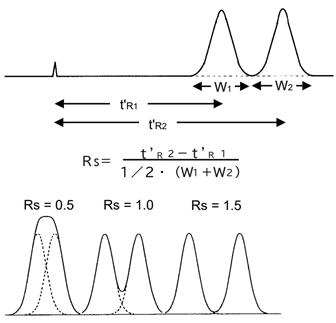
→分離度Rは次の式で表される

R = 2 ( t_R1 – t_R2 ) / ( W₁ + W₂ )

ここでt_R1 , t_R2 はそれぞれピーク1, 2の保持時間、W₁ , W₂ はそれぞれピーク1とピーク2の幅を表す

前述から

前述からLを2倍にするとt_R1 , t_R2 は2倍になり、

W₁ , W₂ は√2倍になるので、

Lが2倍になった時の分離度R’は

R’ = 2 ( 2 t_R1 – 2 t_R2 ) / ( √2 W₁ +√ 2 W₂ )

= 2 × 2 ( t_R1 – t_R2 ) / √2 ( W₁ + W₂ )

= 2√2 ( t_R1 – t_R2 ) / ( W₁ + W₂ )

= √2 R

となり分離度も√2倍になります。

先ほどと同じく複雑なのは多分√2倍で考えても良さそうです。

最後に、理論段相当高さHを表す式(Van Deemterの式)について（令和元年8月問18）

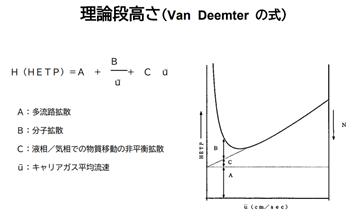
H = A + B / v + C v

ここで各定数は次のこと

A : 渦流拡散（多流路拡散）に起因する定数

B : 成分分子が進行方向に拡散移動（分子拡散）することに起因する定数

C : 移動相と固定相間の平衡の遅れ（非平衡拡散）に起因する定数

v : 移動相の平均線速度

選択肢には各項でA, B, Cにvが乗じられているか、除されているか否かを選択することができればこの手の問題は解けるからこれを整理します。

前述から理論段相当高さはカラムの長さを理論段数で除した値なので小さいほど分離性能が良いです。

つまり乗じられて大きくなる→分離性能が悪くなります。

除されて小さくなる→分離性能が良くなります。

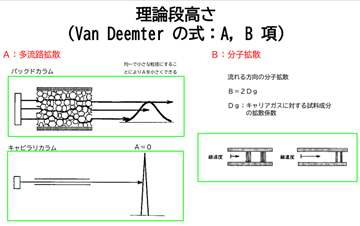
Aについては流路が多数あることによりピークが広がる

ということなので線速度vには関係ありません(A)。

Bについては進行方向への分子拡散であるため

線速度vが大きいほど大きくなり、

分離が悪くなる=Hが大きくなるのでBにvが乗じられます(Bv)。

Cについては移動相と固定相の間の移動に関するものなので、

線速度vが大きいと相互作用せずに通過してしまう

=分離が悪くなる=Hが大きくなることから

Cはvで除されます(C/v)。

長々となりましたが以上、参考になれば幸いです。